Đó là chiếc máy bay của Hãng hàng không Malaysia mất tích ngày 8-3 cùng với 239 hành khách và nhân viên phục vụ.
Từ lúc đấy trở đi đã có không biết bao nhiêu phỏng đoán ly kỳ về số phận chiếc máy bay. Tất cả chấm dứt vào ngày 24-3 khi thủ tướng Malaysia tuyên bố máy bay 370 đã rơi ở vùng biển phía nam Ấn Độ Dương và không ai sống sót cả. Ông cũng nói là kết luận này dựa trên cơ sở “một kiểu phân tích chưa từng được sử dụng trong các cuộc điều tra như thế này”.
Tín hiệu “ping”
Ngay lập tức mọi người và đặc biệt là thân nhân của các hành khách đặt câu hỏi làm thế nào mà ông thủ tướng Malaysia có thể khẳng định như đinh đóng cột như vậy khi chưa tìm thấy bất kỳ mảnh vỡ nào của chiếc máy bay.
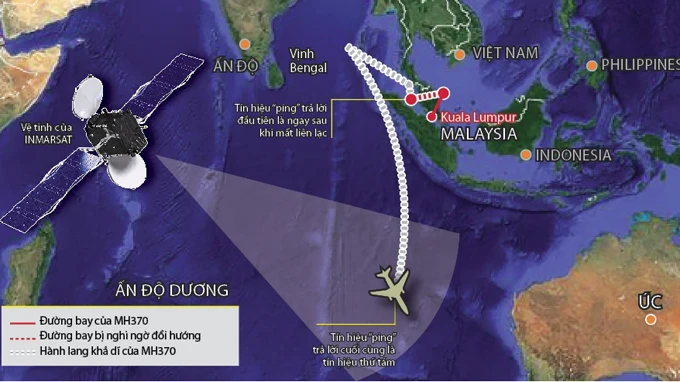
Ai cũng biết rằng toàn bộ liên lạc giữa máy bay và mặt đất đã bị ngắt và các rađa quân sự của Malaysia chỉ cho biết là máy bay đã đổi hướng khi mất tín hiệu. Sau đó là một khoảng trống mênh mông và người ta không có bất cứ dấu vết nào của chiếc máy bay ngoài tám tín hiệu “ping” vô cùng bé nhỏ phát ra từ một thiết bị radio trên máy bay trả lời tín hiệu thăm hỏi của vệ tinh Hãng truyền tin INMARSAT.
Số là các vệ tinh của Hãng truyền tin INMARSAT cứ mỗi tiếng một lần truyền đi một tín hiệu “ping” đến các thiết bị trong hệ thống và các thiết bị này sẽ phát tín hiệu trả lời. Mục đích chỉ để kiểm tra sự thông suốt thông tin. Máy bay 370 có thiết bị thuộc hệ thống INMARSAT. Các phi công không biết thiết bị này trên máy bay sẽ tự động trả lời tín hiệu thăm hỏi của vệ tinh.
Tín hiệu “ping” trả lời đầu tiên là ngay sau khi mất liên lạc với máy bay lúc 1g11 sáng. Tín hiệu “ping” trả lời cuối cùng là tín hiệu thứ tám lúc 8g11 sáng. Như vậy là máy bay còn bay hơn bảy giờ sau đó. Rất tiếc là các tín hiệu này không cho biết vị trí của máy bay.
Tuy nhiên, các nhân viên của Hãng truyền tin INMARSAT có ý tưởng phân tích tám tín hiệu trên bằng các phương pháp toán học để xác định đường đi của máy bay 370. Đây thật sự là một ý tưởng điên rồ. Chúng ta hãy thử tưởng tượng bầu trời rộng lớn ra sao và chúng ta chỉ nhận được tám tiếng “ping” mà không biết chúng từ đâu đến.
Cái hay của thuật toán
Trước tiên, người ta biết khoảng thời gian từ lúc vệ tinh phát đi tín hiệu thăm hỏi cho đến lúc nhận được tín hiệu trả lời từ máy bay. Người ta cũng biết trong một giây thì tín hiệu đi được bao xa. Với những dữ liệu này, người ta tính được khoảng cách từ vệ tinh đến máy bay tại từng thời điểm nhận tín hiệu “ping”.
Rất may là vệ tinh của Hãng INMARSAT là vệ tinh địa tĩnh, có nghĩa là nó luôn nằm ở một vị trí cố định so với Trái đất. Vì thế người ta biết chiếc máy bay nằm trên một cung tròn với tâm là vệ tinh và bán kính là khoảng cách tính được, nhưng không biết tại vị trí nào và nó bay theo phương nào.
Trong khi tìm cách tính toán chính xác khoảng cách trên, người ta lại phát hiện hướng đi của máy bay có thể dự đoán được từ tần số các tín hiệu “ping”. Điều này cũng giống như khi ta nghe tiếng tàu hỏa mà có thể đoán được tàu đang đi từ đâu đến. Lý do là âm thanh sẽ bị nén lại hay nở ra khi tàu chuyển động đến gần hoặc ra xa chỗ đứng của ta.
Tai ta có thể nhận biết được những biến đổi âm thanh này và nhờ đó ta biết hướng tàu chạy. Trong vật lý người ta gọi hiện tượng này là hiệu ứng Doppler.
Dựa theo các nguyên lý trên, nhân viên của Hãng INMARSAT đã lập nên một thuật toán cho phép tính toán hướng đi của chiếc máy bay 370. Thuật toán đã được các chuyên gia hàng không của Anh thẩm định và thử nghiệm. Khi chạy thuật toán này, người ta thấy chiếc máy bay chỉ có thể bay đến vùng biển phía nam Ấn Độ Dương, giống với các dự đoán trước đấy.
Thuật toán tuy không chính xác hoàn toàn nhưng nó cũng cho biết vùng biển cuối cùng nơi máy bay 370 có thể bay đến. Nơi này không có đất liền cho máy bay hạ cánh nên thủ tướng Malaysia mới có thể kết luận là không còn ai trên chiếc máy bay này sống sót sau hai tuần mất tích.
Đó chính là lý do mà trang mạng SLATE chạy tít “Làm thế nào mà toán học có thể xác định được ai đó đã chết?”.
Theo HÀ TRUNG (TTO)






























